Mais algumas questões de Geometria analítica. Hoje as questões (10 com as respectivas respostas) abordam o estudo da Reta. Em caso de dificuldades na resolução de algum exercício contrate uma aula individual pelo e-mail: sovestibular@gmail.com. Bom Estudo ;)
01. (FEI) As retas 2x - y = 3 e 2x + ay = 5 são perpendiculares. Então:
a) a = -1
b) a = 1
c) a = -4
d) a = 4
e) n.d.a.
RESPOSTA: D
02. Determinar a reta perpendicular a 2x - 5y = 3 pelo ponto P(-2; 3).
RESPOSTA: D
03. (USP) A equação da reta que passa pelo ponto (3; 4) e é paralela à bissetriz do 2° quadrante é:
a) y = z - 1
b) x + y - 7 = 0
c) y = x + 7
d) 3x + 6y = 3
e) n.d.a.
RESPOSTA: B
04. Determinar o ponto B simétrico de A(-4; 3) em relação à reta x + y + 3 = 0.
RESOLUÇÃO: B = (-6; 1)
05. Determinar a reta perpendicular à reta de equação x + 2y - 3 = 0 no seu ponto de abscissa igual a 5.
RESOLUÇÃO: 2x - y - 11 = 0
06. Determinar a equação da mediatriz do segmento de extremos A(-3; 1) e B(5; 7).
RESOLUÇÃO: 4x + 3y - 16 = 0
07. As retas (r) 2x + 7y = 3 e (s) 3x - 2y = -8 se cortam num ponto P. Achar a equação da reta perpendicular a
r pelo ponto P.
RESOLUÇÃO: 7x - 2y + 16 = 0
08. As retas 3x + 2y - 1 = 0 e -4x + 6y - 10 = 0 são:
a) paralelas
b) coincidentes
c) perpendiculares
d) concorrentes e não perpendiculares
e) n.d.a.
RESPOSTA: C
09. (USP) A equação da reta passando pela origem e paralela à reta determinada pelos pontos A(2; 3) e B(1; -4) é:
a) y = x
b) y = 3x - 4
c) x = 7y
d) y = 7x
e) n.d.a
RESPOSTA: D
10. Os pontos P(x, y) tais que | x | + | y | = 4 constituem:
a) um par de retas
b) um par de semi-retas
c) o contorno de um quadrado
d) quatro retas paralelas
e) o contorno de um triângulo
RESPOSTA: C
Vamos relembrar alguns conceitos para ajudar a resolver os exercícios:
COEFICIENTE ANGULAR OU DECLIVIDADE DE UMA RETA
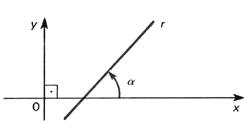
Coeficiente angular (m) de uma reta r não perpendicular ao eixo das abscissas é o número real m que expressa a tangente trigonométrica de sua inclinação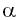 , ou seja: m = tg
, ou seja: m = tg 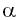

EQUAÇÃO DA RETA
Equação geral da reta
Toda reta do plano possui uma equação da forma: ax + by + c = 0
na qual a, b, c são constantes e a e b não simultaneamente nulos.
Exemplos:
a) – 3x + 2y - 10 = 0
b) 6x – 2y – 11 = 0
Equação reduzida da reta
É toda equação de reta onde a variável y fica isolada. Na equação da reta na forma reduzida podemos identificar o coeficiente angular do lado da variável x e o coeficiente linear (termo independente da equação).
Exemplos:
a) y = 2x – 8
Coeficiente angular = 2
Coeficiente linear = - 8
b) y = – 2x + 7
Coeficiente angular = – 2
Coeficiente linear = 7
CÁLCULO DO COEFICIENTE ANGULAR E DA EQUAÇÃO DA RETA
Para calcular o coeficiente angular (não possuindo o valor da inclinação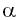 ) e achar a equação da reta, utiliza-se uma única fórmula:
) e achar a equação da reta, utiliza-se uma única fórmula:
ATENÇÃO: A partir da fórmula acima, podemos determinar o coeficiente angular e a equação da reta da seguinte forma:
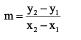
COEFICIENTE ANGULAR OU DECLIVIDADE DE UMA RETA
Coeficiente angular (m) de uma reta r não perpendicular ao eixo das abscissas é o número real m que expressa a tangente trigonométrica de sua inclinação

EQUAÇÃO DA RETA
Equação geral da reta
Toda reta do plano possui uma equação da forma: ax + by + c = 0
na qual a, b, c são constantes e a e b não simultaneamente nulos.
Exemplos:
a) – 3x + 2y - 10 = 0
b) 6x – 2y – 11 = 0
Equação reduzida da reta
É toda equação de reta onde a variável y fica isolada. Na equação da reta na forma reduzida podemos identificar o coeficiente angular do lado da variável x e o coeficiente linear (termo independente da equação).
Exemplos:
a) y = 2x – 8
Coeficiente angular = 2
Coeficiente linear = - 8
b) y = – 2x + 7
Coeficiente angular = – 2
Coeficiente linear = 7
CÁLCULO DO COEFICIENTE ANGULAR E DA EQUAÇÃO DA RETA
Para calcular o coeficiente angular (não possuindo o valor da inclinação
ATENÇÃO: A partir da fórmula acima, podemos determinar o coeficiente angular e a equação da reta da seguinte forma:
Ainda com dúvidas????
Contrate uma aula individual pelo e-mail:
sovestibular@gmail.com









3 comentários:
A QUESTÃO 2 APRESENTA ERRO
Pq?
QUERO COPIAR ESSA PORRA...
Postar um comentário