
Dez questões sobre capacitores com as respectivas respostas para você testar seus conhecimentos em Física Elétrica. No final da postagem você encontra dados teóricos sobre o assunto para reforçar seus estudos ou mesmo auxiliar nos exercícios em que você encontrar dificuldade. Se tiver interesse pode contratar uma aula individual com um de nossos professores especializados. Contatos pelo e-mail: sovestibular@gmail.com. Bom trabalho
01. (PUC - SP) Colocando um corpo carregado positivamente numa cavidade no interior de um condutor neutro, conforme a figura, a polaridade das cargas na superfície externa do condutor, bem como o fenômeno responsável pelo seu aparecimento, serão, respectivamente:
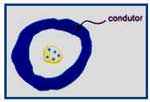
a) negativa; contato.
b) positiva; fricção.
c) negativa; indução.
d) positiva; indução.
e) neutra, pois o condutor está isolado pelo ar do corpo carregado.
RESPOSTA: D
02. (FEI) Quando um corpo eletrizado com carga +Q é introduzido na cavidade de um condutor neutro, oco, este envolvendo completamente aquele sem que ambos se toquem:
a) o condutor oco sempre apresenta cargas cuja soma é nula;
b) a face da cavidade sempre se eletriza com carga +Q;
c) nunca há carga na face exterior do condutor;
d) o potencial do condutor oco é sempre nulo;
e) o potencial do corpo eletrizado sempre se anula.
RESPOSTA: A
03. (ITA - SP) Um condutor esférico oco, isolado, de raio interno R, em equilíbrio eletrostático, tem seu interior uma pequena esfera de raio r < R, com carga positiva. neste caso, pode-se afirmar que:
a) A carga elétrica na superfície externa do condutor é nula.
b) A carga elétrica na superfície interna do condutor é nula.
c) O campo elétrico no interior do condutor é nulo.
d) O campo elétrico no exterior do condutor é nulo.
e) Todas as alternativas acima estão erradas.
RESPOSTA: E
04. (UNISA) Um capacitor plano de capacitância C e cujas placas estão separadas pela distância d encontra-se no vácuo. Uma das placas apresenta o potencial V e a outra -V. A carga elétrica armazenada pelo capacitor vale:
a) CV
b) 2CV
c) V . d
d) 2 V/d
e) CV / d
RESPOSTA: B
05. (MACKENZIE) A capacitância de um capacitor aumenta quando um dielétrico é inserido preenchendo todo o espaço entre suas armaduras. Tal fato ocorre porque:
a) cargas extras são armazenadas no dielétrico;
b) átomos do dielétrico absorvem elétrons da placa negativa para completar suas camadas eletrônicas externas;
c) as cargas agora podem passar da placa positiva à negativa do capacitor;
d) a polarização do dielétrico reduz a intensidade do campo elétrico no interior do capacitor;
e) o dielétrico aumenta a intensidade do campo elétrico.
RESPOSTA: D
06. (PUCC) Um capacitor de placas paralelas com ar entre as armaduras é carregado até que a diferença de potencial entre suas placas seja U. Outro capacitor igual, contendo um dielétrico de constante dielétrica igual a 3, é também submetido à mesma diferença de potencial. Se a energia do primeiro capacitor é W, a do segundo será:
a) 9W
b) W/9
c) 3W
d) W/3
e) n.d.a.
RESPOSTA: C
07. (FEI) Associando-se quatro capacitores de mesma capacidade de todas as maneiras possíveis, as associações de maior e de menor capacidade são, respectivamente:
a) Dois a dois em série ligados em paralelo e dois a dois em paralelo ligados em série.
b) Dois a dois em série ligados em paralelo e os quatro em série.
c) Os quatro em paralelo e dois a dois em paralelo ligados em série.
d) Os quatro em série e os quatro em paralelo.
e) Os quatro em paralelo e os quatro em série.
RESPOSTA: E
08. (MACKENZIE) Uma esfera condutora elétrica tem um diâmetro de 1,8cm e se encontra no vácuo (K0 = 9 . 109 N . m2/C2). Dois capacitores idênticos, quando associados em série, apresentam uma capacitância equivalente à da referida esfera. A capacidade de cada um destes capacitores é:
a) 0,5 pF
b) 1,0 pF
c) 1,5 pF
d) 2,0 pF
e) 4,0 pF
RESPOSTA: D
09. Os quatro capacitores, representados na figura abaixo, são idênticos entre si. Q1 e Q2 são respectivamente, as cargas elétricas positivas totais acumuladas em 1 e 2. Todos os capacitores estão carregados. As diferenças de potencial elétrico entre os terminais de cada circuito são iguais.

Em qual das seguintes alternativas a relação Q1 e Q2 está correta?
a) Q1 = (3/2) Q2
b) Q1 = (2/3) Q2
c) Q1 = Q2
d) Q1 = (Q2)/3
e) Q1 = 3(Q2)
RESPOSTA: E
10. (UEMT) Dois condensadores C1 e C2 são constituídos por placas metálicas, paralelas e isoladas por ar. Nos dois condensadores, a distância entre as placas é a mesma, mas a área das placas de C1 é o dobro da área das placas de C2. Ambos estão carregados com a mesma carga Q. Se eles forem ligados em paralelo, a carga de C2 será:
a) 2Q
b) 3 Q/2
c) Q
d) 2 Q/3
e) Q/2
RESPOSTA: E
Lembretes:
Capacitor
Origem: Wikipédia, a enciclopédia livre
Capacitância
A propriedade que estes dispositivos têm de armazenar energia elétrica sob a forma de um campo eletrostático é chamada de capacitância ou capacidade (C) e é medida pelo quociente da quantidade de carga (Q) armazenada pela diferença de potencial ou tensão (V) que existe entre as placas:A equação acima é exata somente para valores de Q muito maiores que a carga do elétron (e = 1,602 × 10−19 C). Por exemplo, se uma capacitância de 1 pF fosse carregada a uma tensão de 1 µV, a equação perderia uma carga Q = 10−19 C, mas isto seria impossível já que seria menor do que a carga em um único elétron. Entretanto, as experiências e as teorias recentes sugerem a existência de cargas fracionárias.
A capacitância de um capacitor de placas paralelas constituído de dois eletrodos planos idênticos de área A separados à distância constante d é aproximadamente igual a:
- C é a capacitância em faraday
- ε0 é a permissividade eletrostática do vácuo ou espaço livre
- εr é a constante dielétrica ou permissividade relativa do isolante utilizado.
Energia
A energia (no SI, medida em Joules) armazenada em um capacitor é igual ao trabalho feito para carregá-lo. Considere um capacitor com capacitância C, com uma carga +q em uma placa e -q na outra. Movendo um pequeno elemento de carga dq de uma placa para a outra contra a diferença de potencial V = q/C necessita de um trabalho dW:
Os elétrons das moléculas mudam em direção à placa da esquerda positivamente carregada. As moléculas então criam um campo elétrico do lado esquerdo que anula parcialmente o campo criado pelas placas. (O espaço do ar é mostrado para maior clareza; em um capacitor real, o dielétrico fica em contato direto com as placas.)
Circuitos elétricos
Os elétrons não podem passar diretamente através do dielétrico de uma placa do capacitor para a outra. Quando uma tensão é aplicada a um capacitor através de um circuito externo, a corrente flui para uma das placas, carregando-a, enquanto flui da outra placa, carregando-a, inversamente. Em outras palavras, quando a Tensão que flui por um capacitor muda, o capacitor será carregado ou descarregado. A fórmula corrente é dada porNo caso de uma tensão contínua (DC ou também designada CC) logo um equilíbrio é encontrado, onde a carga das placas correspondem à tensão aplicada pela relação Q=CV, e nenhuma corrente mais poderá fluir pelo circuito. Logo a corrente contínua (DC) não pode passar. Entretanto, correntes alternadas (AC) podem: cada mudança de tensão ocasiona carga ou descarga do capacitor, permitindo desta forma que a corrente flua. A quantidade de "resistência" de um capacitor, sob regime AC, é conhecida como reatância capacitiva, e a mesma varia conforme varia a frequência do sinal AC. A reatância capacitiva é dada por:
- XC = reatância capacitiva, medida em ohms
- f = frequência do sinal AC, em Hertz - Hz
- C = capacitância medida em Farads F
É denominada reatância pois o capacitor reage a mudanças na tensão, ou diferença de potencial.
Desta forma a reatância é proporcionalmente inversa à freqüência do sinal. Como sinais DC (ou CC) possuem freqüência igual a zero, a fórmula confirma que capacitores bloqueiam completamente a corrente aplicada diretamente, após um determinado tempo, em que o capacitor está carregando. Para correntes alternadas (AC) com freqüências muito altas a reatância, por ser muito pequena, pode ser desprezada em análises aproximadas do circuito.
A impedância de um capacitor é dada por:
Portanto, a reatância capacitiva é o componente imaginário negativo da impedância.
Em um circuito sintonizado tal como um receptor de rádio, a freqüência selecionada é uma função da indutância (L) e da capacitância (C) em série, como dado em







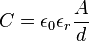




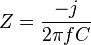
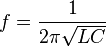





8 comentários:
ótima idéia colocar integral para alunos do ensino médio...
Caro "Anônimo"
Alguns dos melhores livros de ensino médio trazem deduções com ferramentas de cálculo como integrais e derivadas, pois só dessa forma podem ser demonstradas.
Boas escolas de ensino médio também trazem introdução ao cálculo no seu currículo, por isso não achamos que seja necessário omitir esse tipo de informação, que para aqueles que seguirem na área será conhecimento obrigatório
Se não está satisfeito com o conteúdo "gratuito" disponibilizado aqui, garanto que conseguirá informações ao seu nível em sites pagos...
Muito Obrigada, me ajudou bastante!
conhecimento nunca é demais. Se n entende o pq, é pq não é para você ainda ! pense nisso. :D
muito bom , amei ! mas deveria ser mais aprofundado
eu não sei nada disso, queria muuuuito entender na prática de exercícios também :(
vlw
Acho que vai me ajudar na prova de Electricidade Electronica
Postar um comentário